Identities involving trig functions are listed below Pythagorean Identities sin 2 θ cos 2 θ = 1 tan 2 θ 1 = sec 2 θ cot 2 θ 1 = csc 2 θ Reciprocal IdentitiesSec^2 xtan^2 x=3 tan x2tan^2 x 1=3 tan x2 tan^2 x 2 tan^2 x3 tan x1=0 By solving it we are getting two values of tan x that are 1/2 and 1 But the value of 1 will be rejected because tan^1 (1)=45° and for 45° both sin x = tan x and it is provided in the question that the value of sin x is not equal to cos x hence the value of tan x =1/2=0512/2/ Transcript Ex 33, 22 Prove that cot 𝑥 cot 2𝑥 – cot 2𝑥 cot 3𝑥 – cot 3𝑥 cot 𝑥 = 1 Taking LHS cot x cot 2x – cot 2x cot 3x – cot 3x cot x = cot x cot 2x – cot 3x (cot 2x cot x) = cot x cot 2x – cot (2x x) (cot 2x cot x) = cot x cot 2x – ( (cot 2x cot x − 1)/ (cot x cot 2x)) (cot 2x cot x) = cot x cot 2x – (cot 2x cot x – 1) =
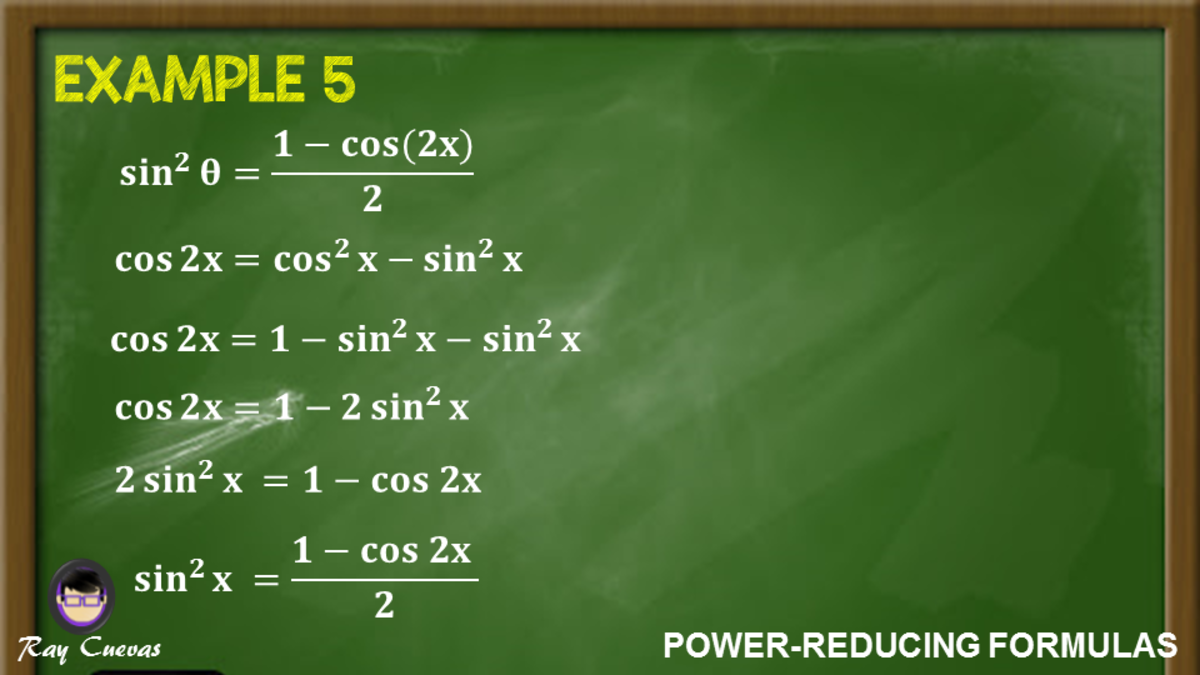
Power Reducing Formulas And How To Use Them With Examples Owlcation
Tan 2x is equal to minus cot x + 5 by 3
Tan 2x is equal to minus cot x + 5 by 3-Tanx = 3cotxtanx = 3×1/tanx(cotx = t/tanx)tan2x = 3tanx = 3 So the value of x will be 60o because the value of tan 60 is 3Get NCERT Exemplar Solutions for Class 11 Chapter Trigonometric Functions here BeTrainedin has solved each questions of NCERT Exemplar very thoroughly to help the students in solving any question from the book with a team of well experianced subject matter experts Practice Trigonometric Functions questions and become a master of concepts
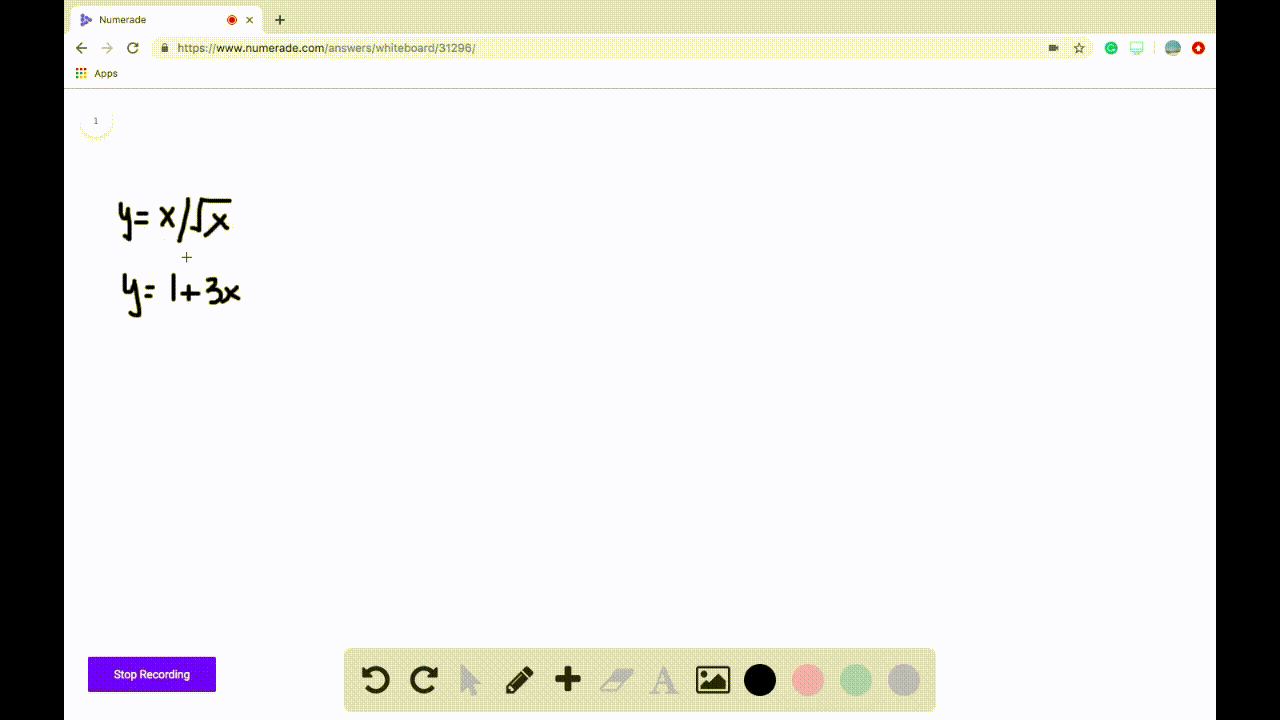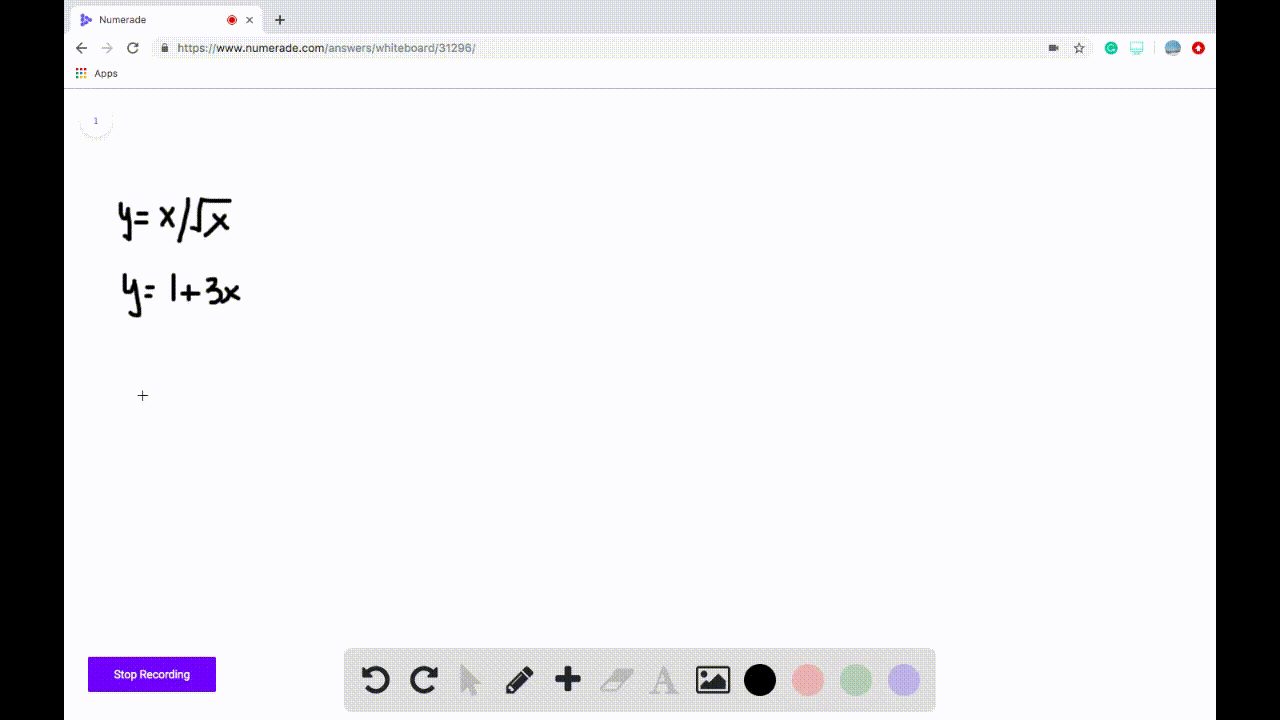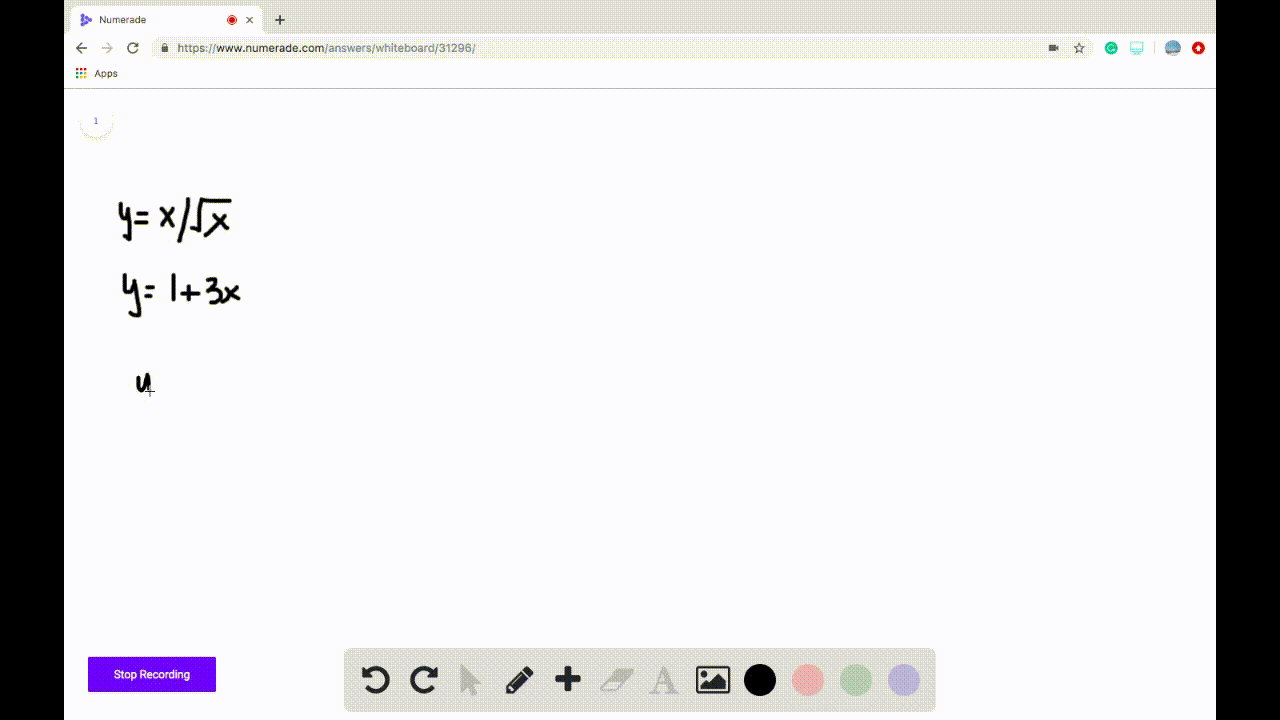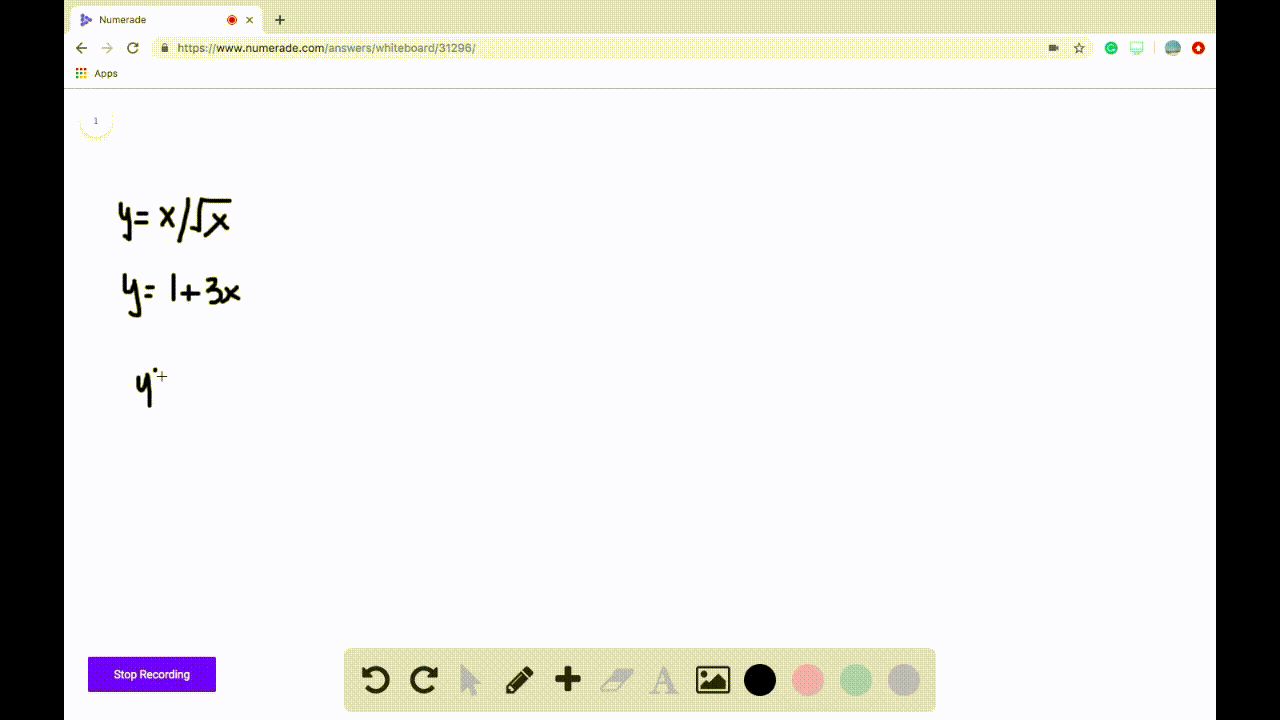



Solved Find All Points On The Curve Y Cot X 0
Tan(x) = square root of 3 Take the inverse tangent of both sides of the equation to extract from inside the tangent The exact value of is The tangent function is positive in the first and third quadrants To find the second solution,13/2/ Example 22 Solve tan 2x = – cot (x" " 𝜋/3) tan 2x = –cot (𝑥" " 𝜋/3) We need to make both in terms of tan Rough tan (90° θ) = –cot θ –cot θ = tan (90° θ) –cot θ = tan (𝜋/2 " θ" ) Replacing θ by x 𝜋/3 –cot ("x " 𝜋/3) = tan (𝜋/2 " x " 𝜋/3) tan 2Plus Gama equals 4/3 And this is a compound angle identity for 10 So using the identity from our formula booklet, this is the same as 10 um, data plus 10 gamma over one minus 10th ada 10 gamma equal 4/3 On we can fill in the sights of 10 data was X 10 gamma is ah one minus X and then one minus 10 Thade is X and tan gamma was one minus X
19/9/ Evaluate ∫(2 tan x – 3 cot x)² dx (a) 4tan x – cot x – 25x C (b) 4 tan x – 9 cot x – 25x C (c) – 4 tan x 9 cot x 25x C (d) 4 tan x 9 cot x 25x C Answer Answer (b) 4 tan x – 9 cot x – 25x CINVERSE TRIGONOMETRIC FUNCTIONS 23 Therefore, tan(cos–1x) = 1–cos θ 21– tanθ = cosθ x x = Hence 2 –1 8 1– 8 17 15 tan cos = 17 8 8 17 = Example 11 Find the value of –1 –59/6/21 For all real values of x, cot x – 2 cot 2x is equal to A tan 2x B tan x C cot 3x D None of these
The integral ∫ π 4 3 π 4 d x 1 cos x is equal to Integrals 8 The area (in sq units) of the region { ( x, y) x ≥ 0, x y ≤ 3, x 2 ≤ 4 y and y ≤ 1 x } is Application of Integrals 9 If ( 2 sin x) d y d x ( y 1) cos x = 0 and y ( 0) = 1, then y ( π 2) is equal to Differential Equations 1017/2/18 Explanation tan2x −cotx = 0 tan2x = cotx tan2x ⋅ tanx = 1 sin2x ⋅ sinx cos2x ⋅ cosx = 1 1 2 ⋅ (cosx − cos3x) 1 2 ⋅ (cos3 cosx) = 1 cosx − cos3x cos3x cosx = 1 cosx − cos3x = cos3x cosx 2cos3x = 0Now, sin 2x = 2tan x/ (1 tan^2 x) , putting tan x = /1 sin 2x = 2 (/1)/ {1 (/1)^2} or, sin 2x = 2 (/1)/2 or, sin 2x = /1 Answer Basically tan theta = cot theta is only possible when theta = 45 degree or (pie/4) radians or odd multiple of that So there are 2 cases



1



Http Www Nhvweb Net Vhs Math Kthompson Files 15 01 5 1 To 5 3 Solutions Pdf
Introduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formulaAnd time was of Minour Square root of three Is actually equal to minus off by by three As for God inverse of court and worst of minus square root of three, it is april two by minus Bye Bye six, which is equal to 5, 5 x six So these are the Values of the expressions that we knowSolve x divided by nine is less than or equal to negative three for x Show your work math When x is divided by 3,the remainder is zIn terms of z, which of the following could be equal to x ?



Scholarworks Gvsu Edu Cgi Viewcontent Cgi Filename 5 Article 1010 Context Books Type Additional




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples
12/5/21 Ex 22, 21 Find value of tan−1 √3 – cot−1 (−√3) Finding tan−1 √𝟑 Let y = tan−1 √3 tan y = √3 tan y = tan (𝝅/𝟑) ∴ y = 𝝅/𝟑 Since range of tan1 is ( (−π)/2,π/2) Hence, Principal Value is 𝝅/𝟑 (Since tan 𝜋/3 = √3) ∴ tan−1 √3 = π/3 Finding cot−1 (−√𝟑) Let x = cot−1 (√3) x = 𝜋 − cot−1 (√3) x = 𝜋 − 𝛑/𝟔 x30/3/16 How do I solve this?A z3 b 3z c 3z d 6z e 92z please answer and explain math Find the exact value of 1 tan 75 degrees 2 Cos 15 degrees 3



Www Berkeleycitycollege Edu Wp Wjeh Files 12 01 Trig Note Circle Approach Pdf




Inttanx Tan2x Tan3x Dx Is Equal To
If y=\sin ^{1} 2 x\tan ^{1} 3 x\cos ^{1} 2 x\cot ^{1} 3 x then (a) y^{\prime}(0)=0 (b) y_{5}=y_{6} (c) y_{2}=y_{A} (d) y_{y}(0)=1 Video Transcript {'transcript' 'in this single correct answer type question given differential equation is that is why dash plus sign off X plus Y overdue is equal to sign off X minus light overdueSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreCot Inverse Calculator Are you looking for a smart tool that calculates the cotangent inverse of a real number or fraction within no time?Then, you have arrived the correct place and our calculator is the best tool that you are looking for The main aim of our Cot Inverse Calculator is to calculate the cotangent inverse of numbers simply and quickly




Tangent And Cotangent Graphs Ck 12 Foundation



Ocw Mit Edu Ans7870 Textbooks Strang Edited Calculus Study Guide 4 Pdf
Given,y = tan21 cos−1( 35 )Let, x= cos−1( 35 )⇒ cosx = 35 ∴ y = tan 21 xy = tan 2x y = 1cosx1−cosx = 1 35 1− 35 = 3 5 3− 5 rationalizing the factor, we get,y = 23− 54) cot2(2x) Answer (3) 2 cot 2x Solution cot x – tan x = (1/tan x) – tan x = (1 – tan 2 x)/tan x Multiplying and dividing by 2, = 2 (1 – tan 2 x)/2 tan x Using the formula tan 2A = 2 tan A/ (1 – tan 2 A), = 2/tan 2x Explanation tan2x −cot2x = sin2(x) cos2(x) − cos2(x) sin2(x) = sin4(x) − cos4(x) cos2(x)sin2(x) = (sin2x cos2x)(sin2x − cos2x) (cos(x)sin(x))2 = (1)( − cos(2x)) 1 4sin2(2x) = − 4 cos(2x) sin2(2x) = − 4csc(2x)cot(2x) Final Answer



Efisd Net Common Pages Displayfile Aspx Itemid




Solve Tan2x Cot X Pi 3 Youtube
General Solution of Tan 5 X = Cot 2 X isTan x cot y/tan x cot y= tan y cot x Math Factorthen use fundamental identities to simplify the expression below and determine which of the following is not equivalent cot^2 a * tan^2 a cot^2 a A csc^ 2 alpha B1/ sin^ 2 alpha C1/ 1cos^ 2 alpha Dsec^ 2 alphaTan 2 θ = sec 2 θ − 1 The square of tan function equals to the subtraction of one from the square of secant function is called the tan squared formula It is also called as the square of tan function identity
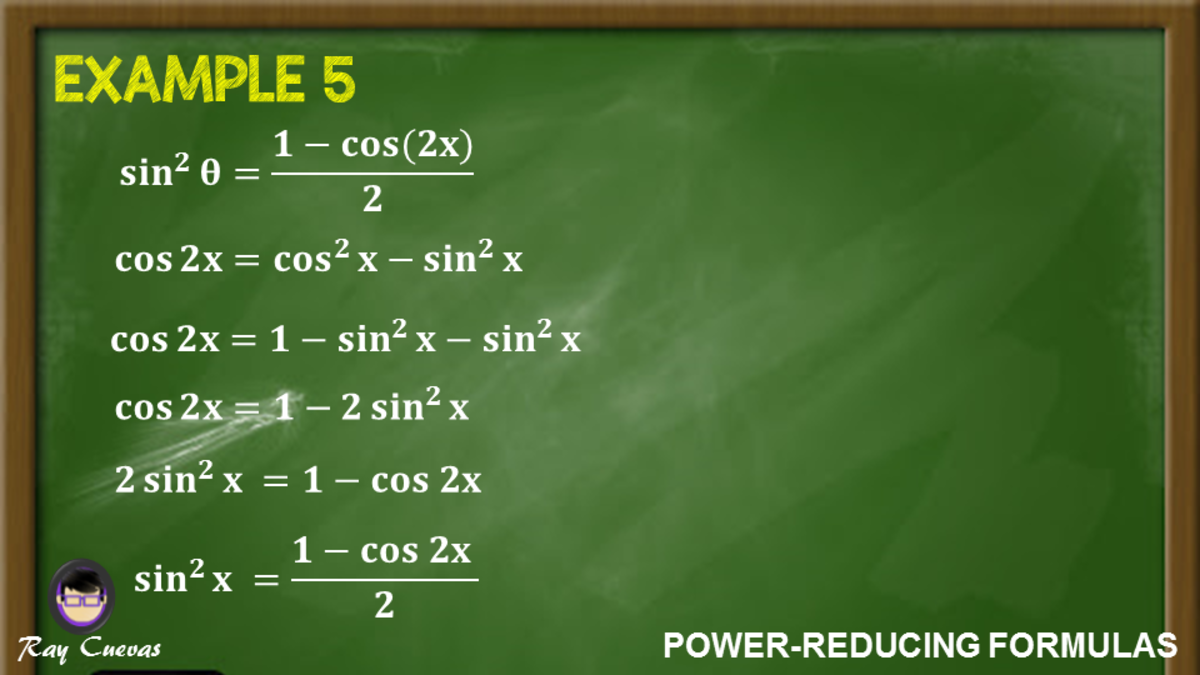



Power Reducing Formulas And How To Use Them With Examples Owlcation




Trigonometry Revise
The answer is =2csc(2x) We need tanx=sinx/cosx cotx=cosx/sinx cos^2xsin^2s=1 sin2x=2sinxcosx cscx=1/sinx Therefore, cotxtanx=cosx/sinxsinx/cosx =(cos^2xsin^2x)/(sinxcosx) =1/(sinxcosx) =2/sin(2x) =2csc(2x)If cot2x =cot(x−y)cot(x −z), then cot2x is equal to (where x =±π/4 )12/5/ X equal to tan a minus tan B and Y equal to COT B minus cot a then 1/x1/y equal to



2




If Y X Cot X Prove That Sin 2 X D 2ydx 2 2y 2x 0
Tan^2x= 2tanxsinx My work so far tan^2x 2tanxsinx=0 tanx(tanx 2sinx)=0 Then the solutions are TanX=0 and sinX/cosX = 2 sin X Divide through by sinX we have to check this later to see if allowed (ie sinX math Prove the identity 1cos2x/sin2x = 1tanx/1cotx I simplified the RS to tanxClick here👆to get an answer to your question ️ If sin^4x 2 cos^4x 3 = 1 5 , then Join / Login maths If 2 s i n 4 x 3 c o s 4 x = 5 1 , then;BITSAT 16 If tan ( cot x) = cot ( tan x), then sin 2x is equal to (A) (2/(2n1)π) (B) (4/(2n1)π) (2/n(n1)π) (D) (4/n(n1)π) Ch BITSAT 16 If tan ( cot x) = cot ( tan x), then sin 2x is equal to (A) (2/(2n1)π) (B) (4/(2n1)π) (2/n(n1)π) (D) (4/n(n1)π) Ch Tardigrade




If Tan X Cot X 2 Find The Value Of Tan2 X Cot2 X Brainly In



Web Auburn Edu Holmerr 1617 Textbook Lhopital Print Pdf
25/7/19 The value of is option 2) Stepbystep explanation We have, To find, the value of ∴ Using identity, ∵ Using trigonometric identity, Hence, the value of is option 2)Solve the equation 4 tan^2 x 12 sec x 1 =0, for 0 degrees is less than or equal to x is less than or equal to 360 degrees trig tan^2theta6=sec^2theta5 calculus a bridge is 10 m above a canal A motorboat going 3 m/sec passes under the center of the bridge at the same instant that a woman walking 2 m/sec reaches that point30/5/ If cos^2x cos^4x =1 , then the value of tan^4x cot^4x tan^2x cot^2x is equal to ?



2



Http Mr Choi Weebly Com Uploads 1 7 0 5 Mhf4u1 Assignment Chapter 4 B Solutions Pdf
Trigonometry Solve for x cot (x10)=tan (4x) cot (x − 10) = tan (4x) cot ( x 10) = tan ( 4 x) Move all terms containing x x to the left side of the equation Tap for more steps Subtract tan ( 4 x) tan ( 4 x) from both sides of the equation cot ( x − 10) − tan ( 4 x) = 0 cot ( x 10) tan ( 4 x) = 0 Simplify the left side of theWe have, 3tan−1xcot−1x= π⇒ 2tan−1 x(tan−1xcot−1x)= π⇒ 2tan−1 x 2π = π, ∵ tan−1xcot−1x = 2π is an identity⇒ 2tan−1 x= π− 2π = 2π ⇒ tan−1x = 4π ∴ x= tan 4π =123/3/18 If 3 tan1 x cot1 x = π, then x equals (a) 0 (b) 1 (c) 1 (d) 1/2 Questions from AIIMS 10 1 An alternating current i in an inductance coil varies with time according to



Stemeducationjournal Springeropen Com Track Pdf 10 1186 S 015 0029 5 Pdf




1 Tanx Tan X 2 Secx Tanx Cotx 2 1 Prove It Brainly In
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor28/8/ If cot x equal to minus 3 by 5 x in 2 quadrant then find sinx by 2 cos x by 2 tan x by2 1 Log in Join now 1 Log in Join now Ask your question janvi3295 janvi3295 Math Secondary School #tan 2x = (2tan x)/(1 tan^2 x)# (Trig identity) #2/(tan 2x) = (1 tan^2 x)/tan x = 1/(tan x) tan^2 x/(tan x) =# #= cot x tan x#




The Expression Tan X Pi 2 Cos 3pi 2 X Sin 3 7pi 2 X Cos X Pi 2 Tan 3pi 2 X Simplifies To A Brainly In



2
1) when the expression 4x^23x8 is divided by xa, the remainder is 2 find the value of a 2) the polynomial 3x^3mx^2nx5 leaves a remainder of 128 when divided by x3 and a remainder of 4 when divided by x1 calculate the remainder when the Algebra 2Math\sin^2x\cos^2x=1/math math\implies\dfrac{\sin^2x}{\cos^2x}\dfrac{\cos^2x}{\cos^2x}=\dfrac{1}{\cos^2x}/math math\implies\left(\dfrac{\sin x}{\cos xGiven \tan x \cot x = 3 and x is in first quadrant Find \sin x Given tanxcotx = 3 and x is in first quadrant Find sinx Method 1 Recall that \sin (2x) = 2\sin (x)\cos (x) From what you have we have \sin (x) \cos (x) = \dfrac13 \implies \sin (2x) = \dfrac23 Since x lies in the first quadrant, 2x




Solution Solve For X In The Given Equation Arc Tan 2x Arctan X P




Tangent And Cotangent Graphs Ck 12 Foundation
For the first term in equation (1) on the right, we'll use the basic trigonometric identity cot x = 1/tan x as follows (2) = {sin² x/ 1 (1/tan x)} cos² x/ (1 tan x) (3) = {sin² x/ (tan x 1)/tan x)} cos² x/ (1 tan x) Dividing fractions in the first term, we getA tan 2 x = 3 29/1/18 This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Divide both side by cos2x and we get sin2x cos2x cos2x cos2x ≡ 1 cos2x ∴ tan2x 1 ≡ sec2x ∴ tan2x ≡ sec2x − 1 Confirming that the result is an identity



Http Www Madeiracityschools Org Userfiles 194 Classes Chapter 4 pages 129 161 Pdf




Tanx 3 Cotx 5 Secx Trigonometric Quadratic Equation Test Youtube



Ovingtonclassroom Weebly Com Uploads 1 0 6 2 Chapter 4 Review Key Pdf




If A Sec X Tan X And B X Cot X Then Show That Ab A B 1 0



How Can We Prove That 1 Cos4x Cotx Tanx 1 2sin4x Quora



Selectividad Intergranada Com Bach Functions Chapter 6 Pdf



2




If Sin X 2sqrt 6 5 And X Lies Quadrant Iii Find The Values Of Cos X And Cot X




Rd Sharma Solutions For Class 11 Chapter 5 Trigonometric Functions Exercise 5 2 Avail Free Pdf



Http Studentsonline Btps Ca Documents General Session 6 Answer Key Pdf



Tan2x Sec2x ただの悪魔の画像




Graph Of Y Tan X Video Trigonometry Khan Academy




How Do You Prove That Tanx Secx 1 Tanx Secx 1 1 Sinx Cosx Socratic
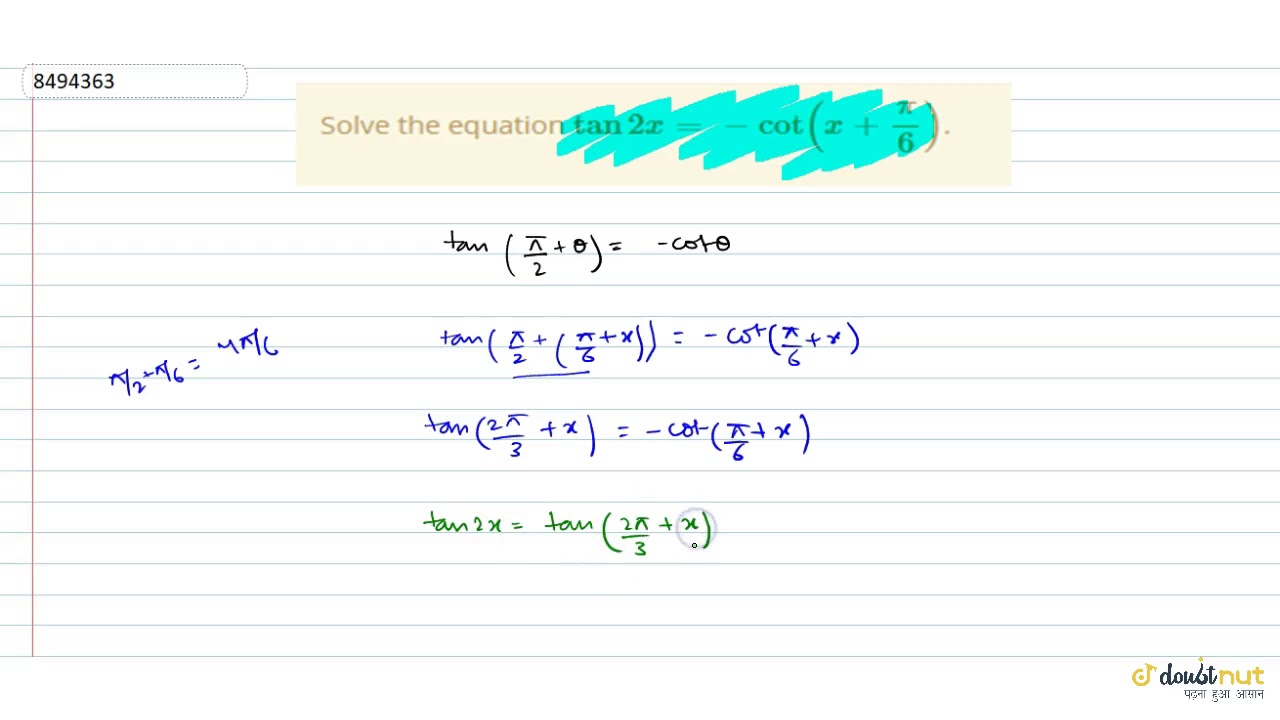



Solve The Equation Tan 2x Cot X Pi 6 Youtube




Cot X Cos 2 X Tan X Sin 2 X 2 Cot 2x Youtube



Faculty Atu Edu Mfinan Trigbook Pdf




Using Trigonometric Identities Video Khan Academy




Example 13 Solve Tan 1 2x Tan 1 3x Pi 4 Class 12




Graphs Of The Other Trigonometric Functions Precalculus Ii



Pmt Physicsandmathstutor Com Download Maths A Level C3 Topic Qs Edexcel Set 1 C3 trigonometry trigonometric identities Pdf




Ex 3 2 3 If Cot X 3 5 Find Values Of Other Trigonometric



Http Staffordhs Ss8 Sharpschool Com Common Pages Userfile Aspx Fileid




Rd Sharma Solutions For Class 11 Chapter 5 Trigonometric Functions Exercise 5 2 Avail Free Pdf



3



Http Ruckdeschel Pbworks Com W File Fetch Chapter 05 Pdf




Trigonometric Identities And Equations
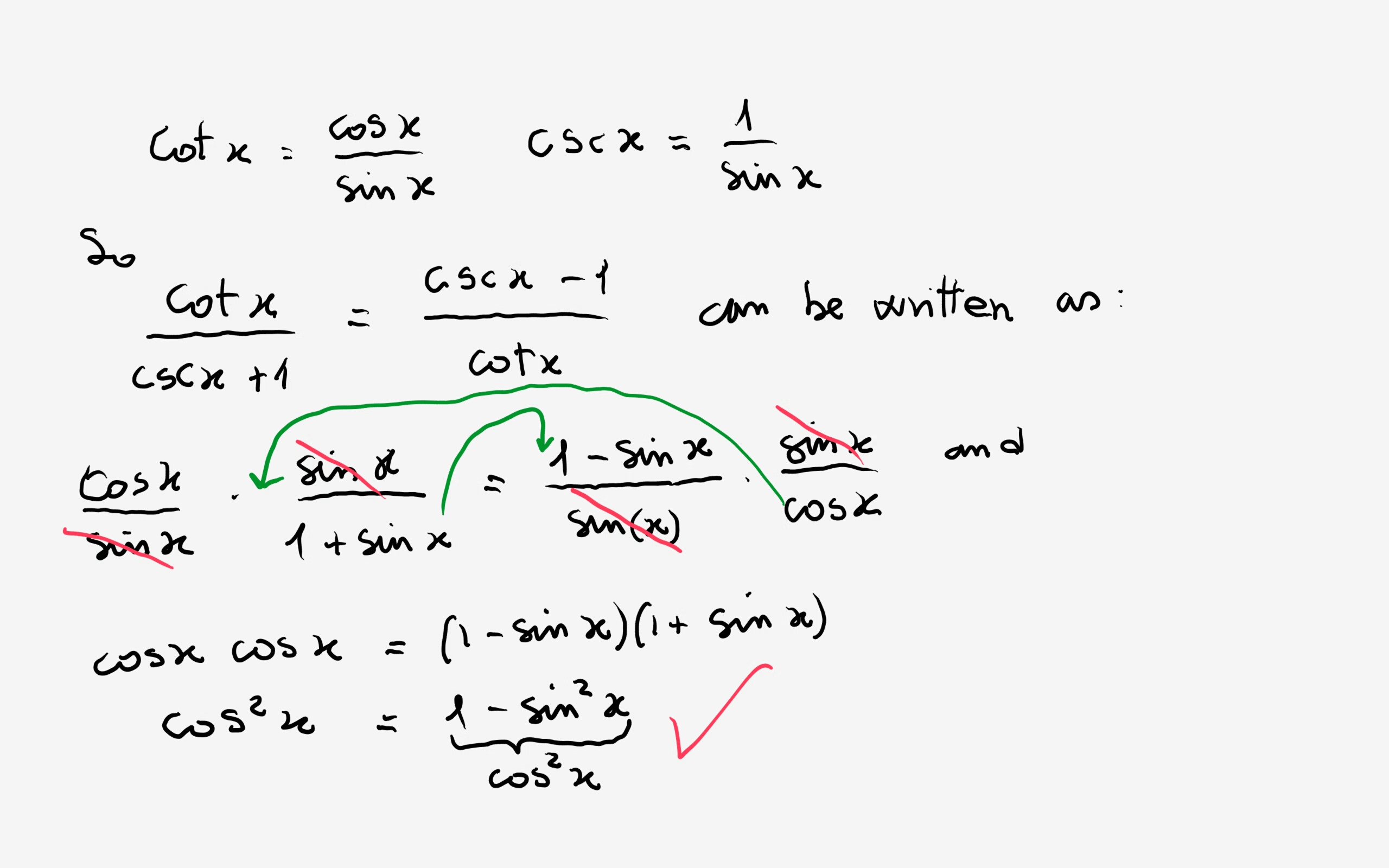



How Do You Verify The Identity Cot X Csc X 1 Csc X 1 Cot X Socratic



Www Thatonemathguy Com Uploads 7 0 1 3 Precalculus 2nd Edition Part 2 Pdf




1 Cos2x




Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 2 3 By Ayman Alam Issuu




Trigonometry Revise
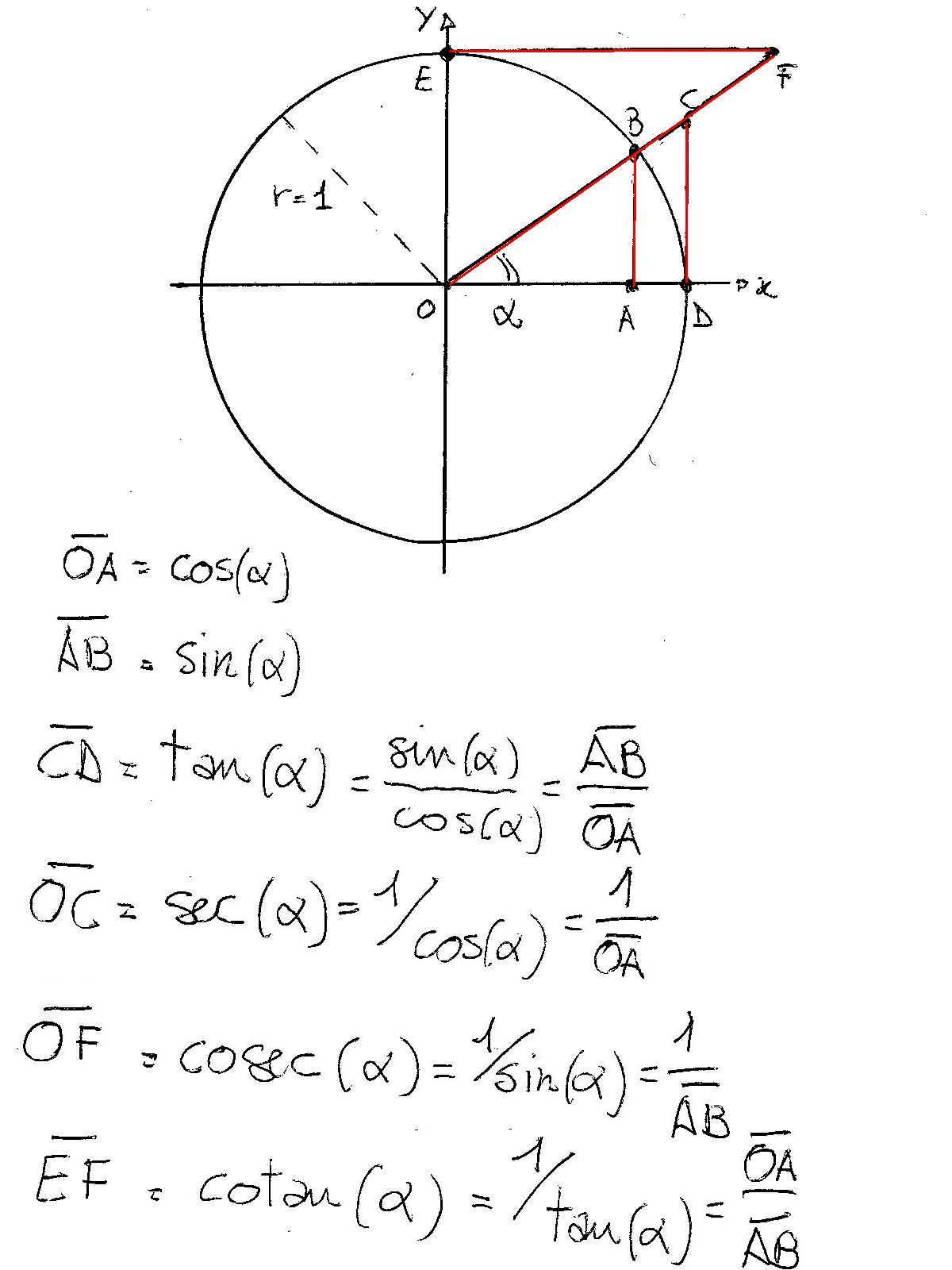



Basic Trigonometric Functions Trigonometry Socratic




Capital Persecution Mass Cot X Pi 2 Burlingtoncode Org




最も欲しかった Tan 2x 1616 Tan 2x 2tanx 1 Tan 2x



Http Ncert Nic In Ncerts L Kemh103 Pdf




Pdf Telecharger Double Angle Identities Gratuit Pdf Pdfprof Com
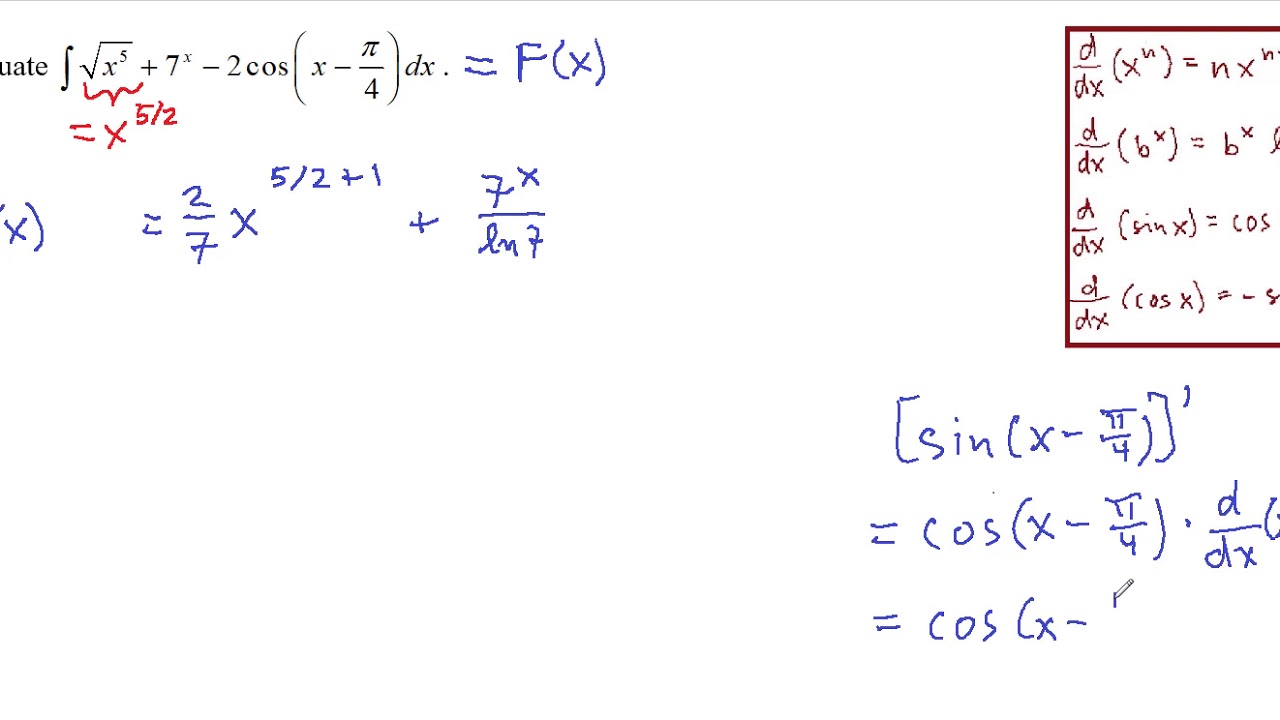



Indefinite Integrals




Solved Find All Points On The Curve Y Cot X 0




Tan 2x Cot 2x 2 Youtube




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples




Power Reducing Formulas And How To Use Them With Examples Owlcation




Solve Tan2x Cot X Pi 3




Trigonometry Workbook For Dummies Pages 151 0 Flip Pdf Download Fliphtml5




Rd Sharma Solutions For Class 11 Chapter 5 Trigonometric Functions Exercise 5 2 Avail Free Pdf




Solve The Trigonometric Equation Tan 2x Cot X Pi 3 Youtube




Examples With Trigonometric Functions Even Odd Or Neither Video Lessons Examples And Solutions



2



How To Evaluate Lim X 0 Cot X Sin 2x Quora




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




If Y Tan 1 Cot X Cot 1 Tan X Then Find Dydx
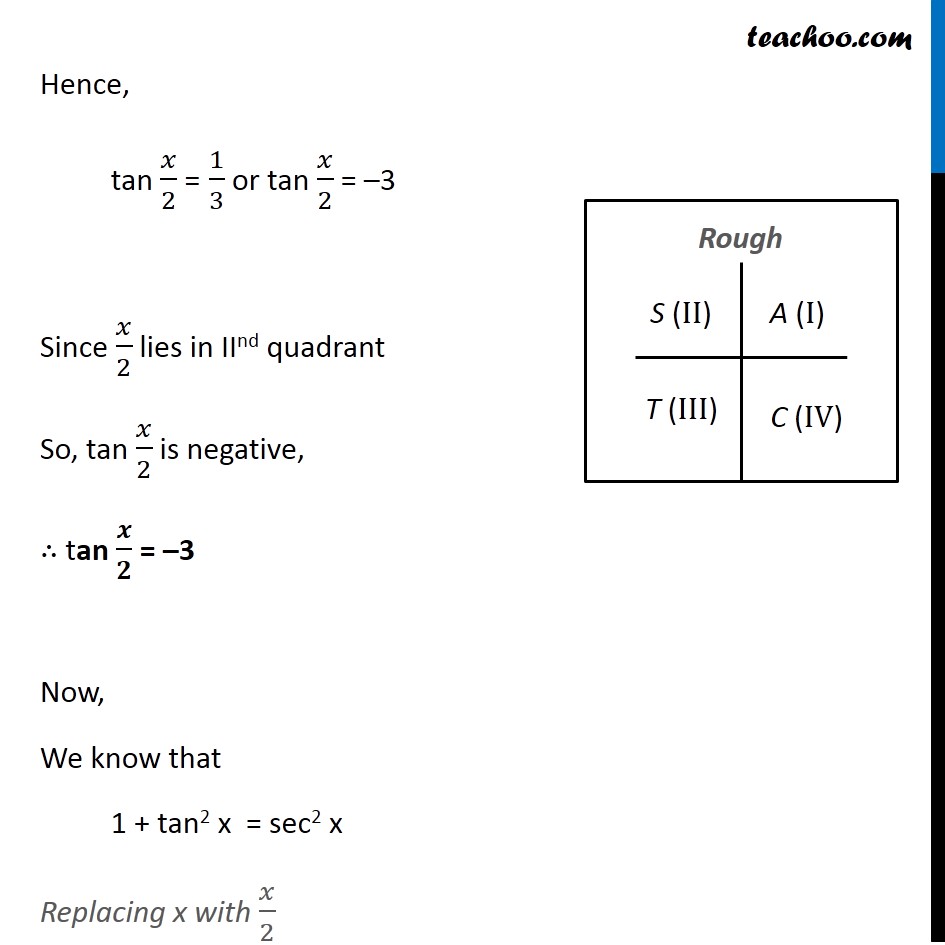



Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2



1



Http Www Willmar K12 Mn Us Cms Lib07 Mn Centricity Domain 273 Double and half angle formulas hw Pdf



Jscholarship Library Jhu Edu Bitstream Handle 1774 2 Pdf Sequence 416 Isallowed Y



Http Www Newpaltz K12 Ny Us Cms Lib Ny Centricity Domain 132 Text 5 6 answers ap rogo et Tsm Pdf



2




Solve Tan2x Cot X P 3 Brainly In



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 5 6 Pdf



2




Derivatives Of Tan X And Cot X Video Khan Academy



Www Carroll Edu Sites Default Files Content Academics Mathematics Mathtexts Activities And Clickers Pdf




The Expression 1 Tan X Tan 2 X 1 Cot X Cot 2 X Has The Positive Values For X Given By



Functions Wolfram Com Introductions Pdf Cot Pdf



Precalculus Flippedmath Com Uploads 1 1 3 0 Pc 10 2 Solutions Pdf



1



Www Cimt Org Uk Projects Mepres Alevel Fpure Ch2 Pdf




Tan2x Sec2x ただの悪魔の画像
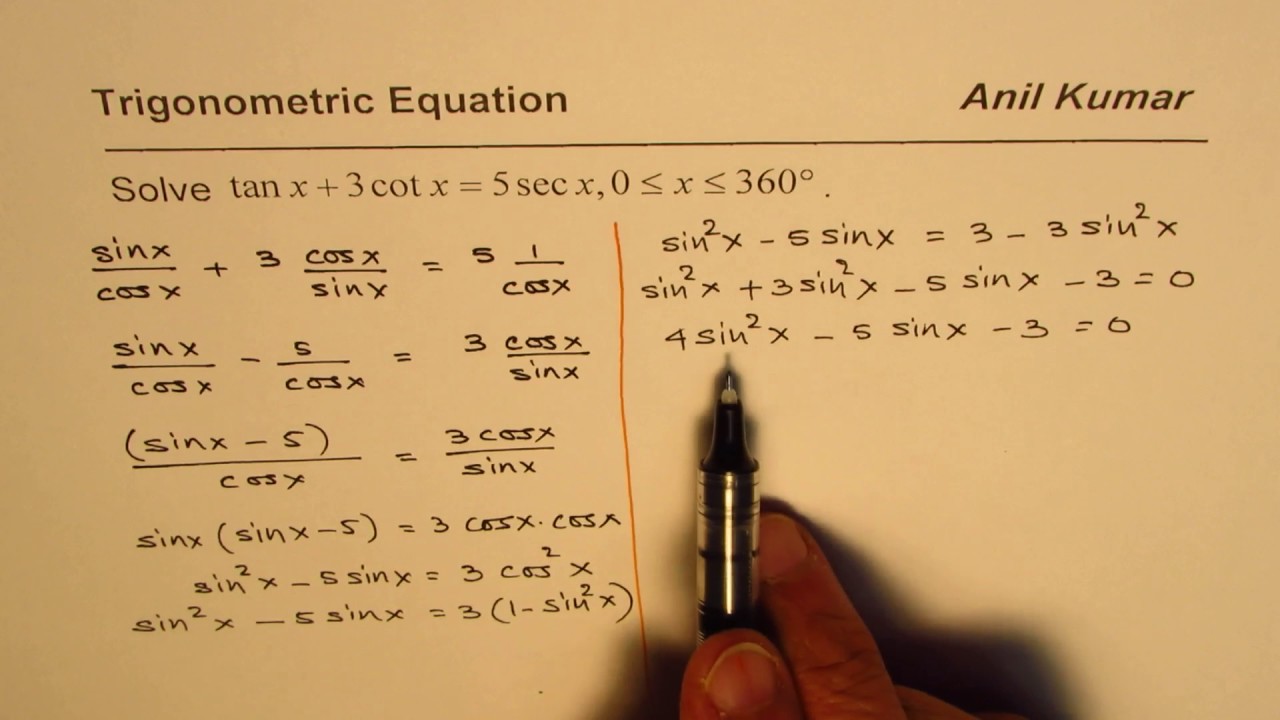



Trig Equation Tanx Plus 3 Cot X Equals 5 Sec X Youtube




Tan 1 2 Cos 1 Square Root 5 3 Maths Inverse Trigonometric Functions Meritnation Com




Solve Tan X Tan 2x Sqrt 3 Tan X Tan 2x Sqrt 3



Capital Persecution Mass Cot X Pi 2 Burlingtoncode Org



Jscholarship Library Jhu Edu Bitstream Handle 1774 2 Pdf Sequence 416 Isallowed Y



Trigonometry Reciprocal Identities Expii



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 5 6 Pdf



Ocw Aprende Org Courses Mathematics 18 01sc Single Variable Calculus Fall 10 1 Differentiation Part A Definition And Basic Rules Problem Set 1 Mit18 01sc Pset1sol Pdf




Chapter 19 Further Integration Pages 1 37 Flip Pdf Download Fliphtml5



Jscholarship Library Jhu Edu Bitstream Handle 1774 2 Pdf Sequence 416 Isallowed Y
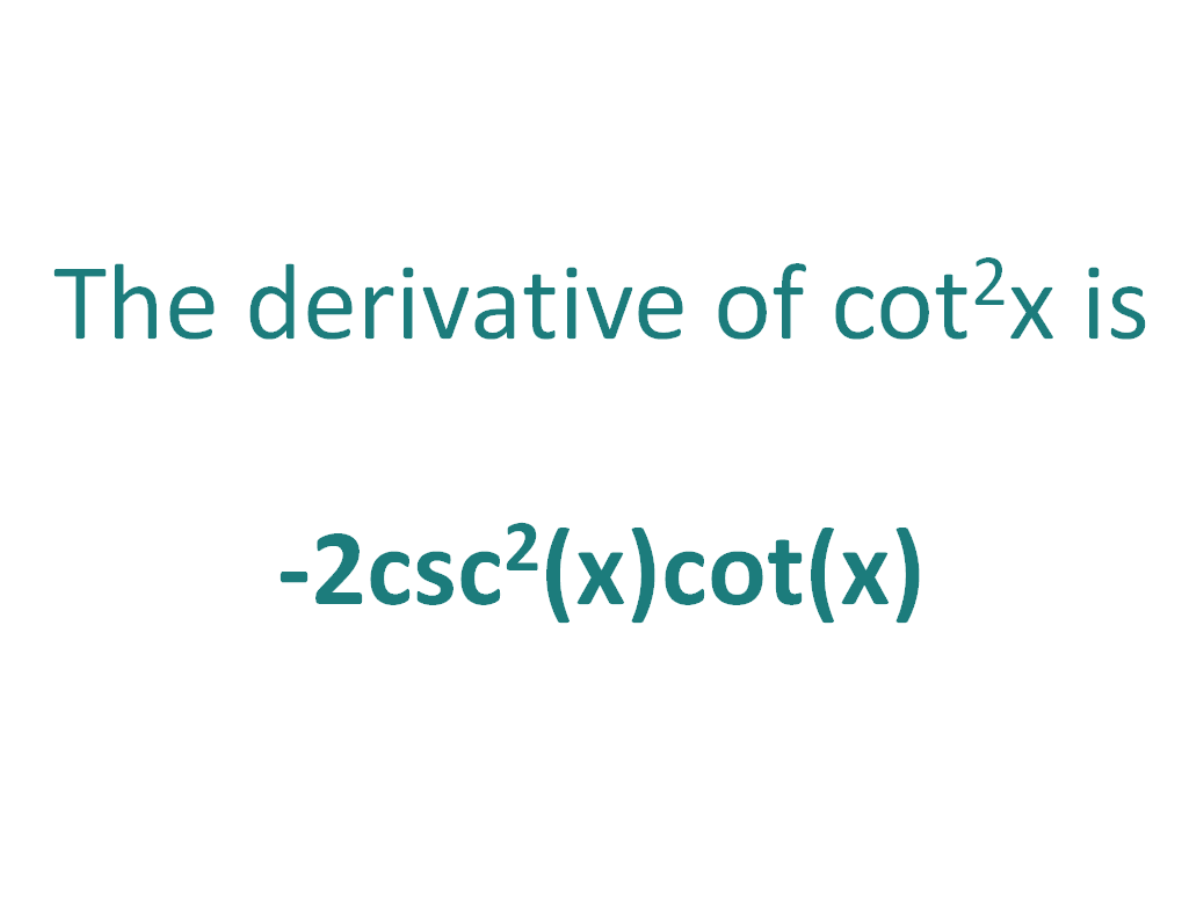



The Derivative Of Cot 2x Derivativeit




Find Sin2x Cos2x And Tan2x If Cosx 5 13 And X Terminates In Quadrant Ii Wyzant Ask An Expert



0 件のコメント:
コメントを投稿